We study properties of the
truncated kernel function 
defined on integers
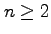
by
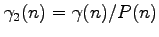
, where
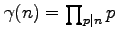
is the well-known
kernel function and
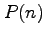
is the largest prime factor of
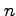
. In particular, we show that the maximal order of
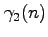
for

is
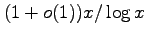
as
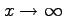
and that
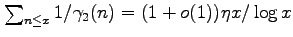
, where

. We further show that, given any positive real number
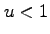
,
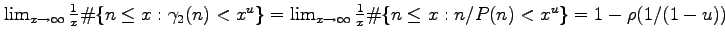
, where

is the Dickman function.
We also show that
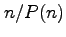
can very often be much larger than
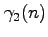
, namely by proving that, given any
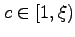
, where
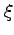
is the unique solution to
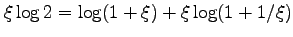
, then