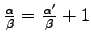
We develop techniques that can be applied to find solutions to the recurrence . Many interesting combinatorial numbers, such as binomial coefficients, both kinds of Stirling and associated Stirling numbers, Lah numbers, Eulerian numbers, and second-order Eulerian numbers, satisfy special cases of this recurrence. Our techniques yield explicit expressions in the instances , , and , adding to the result of Neuwirth on the case . Our approach employs finite differences, continuing work of the author on using finite differences to study combinatorial numbers satisfying simple recurrences. We also find expressions for the power sum for some special cases of the recurrence, and we prove some apparently new identities involving Stirling numbers of the second kind, Bell numbers, Rao-Uppuluri-Carpenter numbers, second-order Eulerian numbers, and both kinds of associated Stirling numbers.