Abstract:

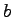
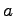
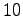
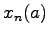
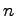
We study the solutions of the equation $a^x\equiv x \left(\text{mod }b^{n}\right)$. For some values of $b$, the solutions have a particularly rich structure. For example, for $b=10$ we find that for every $a$ that is not a multiple of $10$ and for every $n\geq 2$, the equation has just one solution $x_n(a)$. Moreover, the solutions for different values of $n$ arise from a sequence $x(a)= \{x_{i}\}_{i\geq 0}$, in the form $x_n(a)=\sum_{i=0}^{n-1} x_i 10^i$. 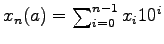For instance, for $a=8$ we obtain

$$8\,^{56} \equiv 56 \left(\text{mod }10^2\right),\quad \qquad 8\,^... ... \quad\qquad 8\,^{5856} \equiv 5856 \left(\text{mod }10^{4}\right),\quad \dots$$

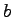
In this paper we prove these results and provide sufficient conditions for the base $b$ to have analogous properties.