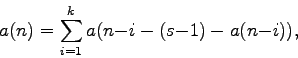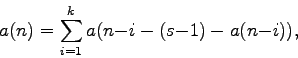This paper is concerned with a family of
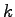
-ary meta-Fibonacci sequences
described by the recurrence relation
where
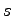
may be any integer, positive or negative.
If
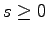
, then the initial conditions are
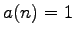
for
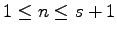
and
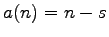
for
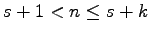
.
If
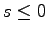
, then the initial conditions are
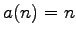
for
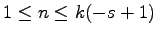
.
We show that these sequences arise as the solutions of two natural counting
problems: The number of leaves at the largest level in certain
infinite
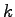
-ary trees, and (for
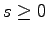
)
certain restricted compositions of an integer.
For this family of generalized meta-Fibonacci sequences and two
families of related sequences we derive combinatorial bijections,
ordinary generating functions,
recurrence relations, and asymptotics (
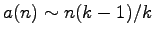
).
We also show that these sequences are related to a
``self-describing" sequence of Cloitre and Sloane.