Let

and
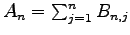
with
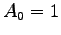
be,
respectively, the
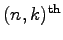
partial and the
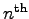
complete
Bell polynomials with indeterminate arguments
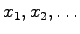
.
Congruences for
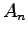
and

with respect to a prime number have
been studied by several authors. In the present paper, we propose
some results involving congruences for

when the arguments
are integers. We give a relation between Bell polynomials and we apply it
to several congruences. The obtained congruences are
connected to binomial coefficients.