Journal of Integer Sequences, Vol. 1 (1998), Article 98.1.3

Abstract: We present a method for computing some numbers bit by bit using only a ruler and compass, and illustrate it by applying it to arctan(X)/π. The method is a spigot algorithm and can be applied to numbers that are constructible over the unit circle and the ellipse. The method is precise enough to produce about 20 bits of a number, that is, 6 decimal digits in a matter of minutes. This is surprising, since we do no actual calculations.

Keywords: Binary expansion, A004715 of the On-Line Encyclopedia of Integer Sequences, constant, ruler and compass construction, π.

 

1. Introduction

 

It is known that rational numbers of the form 1/q can be computed with a ruler and compass in small bases. See [4] for details. The rational numbers computable by this method are precisely those for which q is the number of sides of a regular polygon that can be constructed with ruler and compass; that is, q must be a product of distinct Fermat numbers that are primes [5], see also the Treasure Trove of Mathematics.

 

From those facts, one can ask: are there other points on the unit circle that can be constructed? The answer is obvious: any line constructed on the plane that crosses the unit circle somewhere defines a point from which the binary expansion can be calculated. We understand here that we consider the arc length compared to the unit circle. When we consider a rational number like 2/3 we mean in fact exp(2*π*I*2/3), that is, the arc length of 2/3 compared to 2*π on the unit circle. By taking a simple construction of the angle arctan(1/2) then get an arc length of arctan(1/2)/π = 0.147583.... A number that we believe should be at least irrational. We also remark that the point defined by the angle of arctan(1/2) has algebraic coordinates (2/5*sqrt(5) and 1/5*sqrt(5)), and that this point (on the unit circle) is apparently not a rational multiple of π. We do not know if there is a proof that this number is irrational.

 

Second, the arctan function is a log (with complex values) and π is also a log with complex values. This means that our construction is a ratio of logarithmic values.

 

2. The construction of arctan(1/2)/π and the computation

 

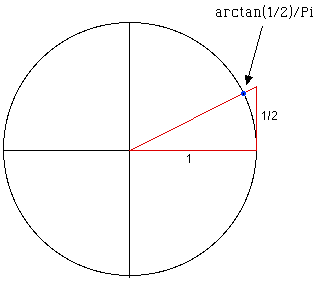
The coordinates of the blue dot are (2/5*sqrt(5), 1/5*sqrt(5)).

Each subdivision of the circle is equivalent to a rational point, here π/2 is 0.01 in binary = 1/4.

 

 

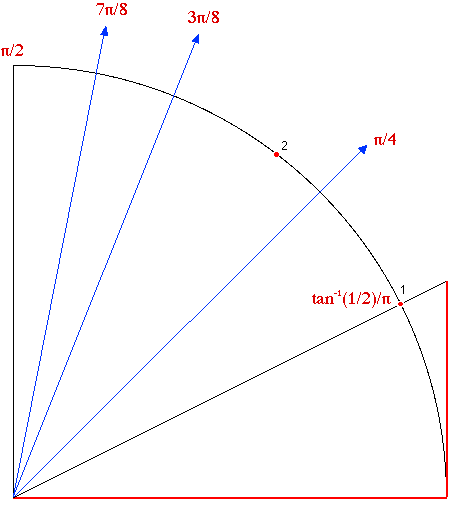
Only the first quadrant is necessary for the computation, see the construction after 11 steps.

 

 

At each step we double the angle and when the point falls in the first quadrant we take the sign of the angle. If the sign is + then we set that the corresponding bit value is 0 and 1 when the sign of the angle is -. By doing it by hand for real, errors accumulate and eventually there is an ambiguity in the sign since at each step there is an uncertainty about the exact position of the point. The limit is somewhere around 20 bits. I could easily produce (with little care) the first 17 bits of the number arctan(1/2)/π. Note: the construction is done on a plain white paper and could be done on the sand in fact with small precision.

 

 

3. Other numbers.

 

Since we can compute any point that lies on the unit circle then any construction that cuts that circle is computable. This includes numbers of the form arctan(A)/π where A is algebraic and constructible with a ruler and compass. According to Borwein and Girgensohn [2], it is possible to compute bit by bit a number like such as (3)/log(2), but the geometrical construction necessary for that implies the use of a rectangular grid Z x Z.

 

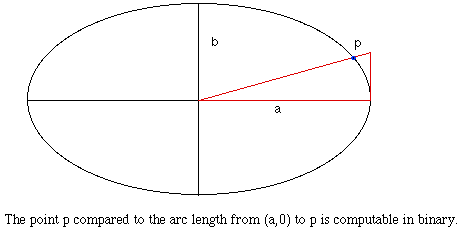
4. Application to the ellipse

 

 

The properties of the circle are not unique, it is also shared with the ellipse and the lemniscate. In this context it means that if we can construct an angle that crosses the ellipse of ratio a/b then we can compute the binary expansion of the position of that point compared to the arc length of the ellipse. The same can be applied to the lemniscate.

 

5. An experimental approach to search for other solutions

 

The next step in this is to ask whether we can combine values of arctan(X)/π to produce other numbers like sqrt(2). From the classical theory of π (Lindemann's proof of the transcendence of π), it is not possible to get 1/π from a geometrical construction. In this context it means that we can't construct an arc length of 1 radian with the ruler and compass. 1 radian has an arc length of 1/π. It would mean that we can construct the number sin(1) and cos(1). The only way I see to produce an example is to try experiments with values of arctan(X)/π where X is a constructible algebraic number.

 

We have to understand here that we deal with an inverse problem. The equation arctan(1/2)+arctan(1/3) = π/4 translates (in arc length), to 1/8 in binary. π/4 = arctan(1) and this number has an arc length of 1/8 compared to the full circle of 2*π.

 

Open questions

 

Can this process could be applied to other types of numbers? (Like sqrt(2)).

Since we can use the first quadrant only (and not a full circle), can we extend this idea to have only a very small portion of the unit circle and push the precision of the computation further?

Are there any simpler number? Or in other words: Is arctan(1/2)/π the simplest example?

Is arctan(1/2)/π an irrational number? (Hint: π/4 = arctan(1/2)+arctan(1/3) and we know that π is irrational).

Is there a bit pattern in arctan(1/2)/π? Is the binary expansion of that number in fact a rule for constructing something that we do not know? See sequence A004715 of the E.I.S.

 

 

6. Bibliography

 

 

[1] Simon Plouffe, work done during the years 1974 to 1983.

 

[2] J. M. Borwein and R. Girgensohn, Addition theorems and binary expansions, Canadian J. Math. 47 (1995) 262-273.

 

[3] Plouffe's constant at the site: Favorite Mathematical Constant of Steve Finch, 1996.

 

[4] Simon Plouffe, The reflection of light rays in a cup of coffee or b^n mod p, Conference, Hull (Canada), October 21, 1979, Congrès des Mathématiciens du Québec.

 

[5] C. R. Hadlock, Field Theory and Its Classical Problems (Carus Mathematical Monographs, No. 19), 1979.

 

[6] N. J. A. Sloane and S. Plouffe, The Encyclopedia of Integer Sequences. San Diego, Calif.: Academic Press, 1995. Also see the On-Line Encyclopedia of Integer Sequences.

 

(Related to sequences A004715 and A028999 .)

Received Jan. 1, 1998; published in Journal of Integer Sequences Jan. 30, 1998.